Decomposition Methods for Mixed-integer Optimal Control ongoing

In this project, we study domain decomposition approaches for optimal control in gas transport networks. Our goal is to couple space-time-domain decomposition with machine learning and mixed-integer programming. We will develop NeTI (Network Tearing and Interconnection), a data-driven and physics-informed algorithm combining mixed-integer nonlinear programming, surrogate model learning, and graph decomposition strategies.

TRR-154 A05
Jan 2022 to Jun 2026
3
2

🧑‍🎓 Project Members

Sebastian Pokutta
Principal Investigator
pokutta (at) zib.de
Kartikey Sharma
kartikey.sharma (at) zib.de
Konrad Mundinger
mundinger (at) zib.de

🪙 Funding

This project is being funded by the Sonderforschungsbereich (SFB) Transregio 154 from January 2022 to June 2026.

🔬 Project Description

Our goal in this project is to integrate decomposition approaches with machine learning based surrogate models in order to solve gas transport problems. The general idea is to decompose as gas network into multiple pieces and then to model the pieces either using the mixed integer program or using machine learning based models. As such this projects has multiple directions. This includes the development of surrogates in order to model part of a network, and the development of decomposition based optimization techniques to actually solve the overall optimization problem. 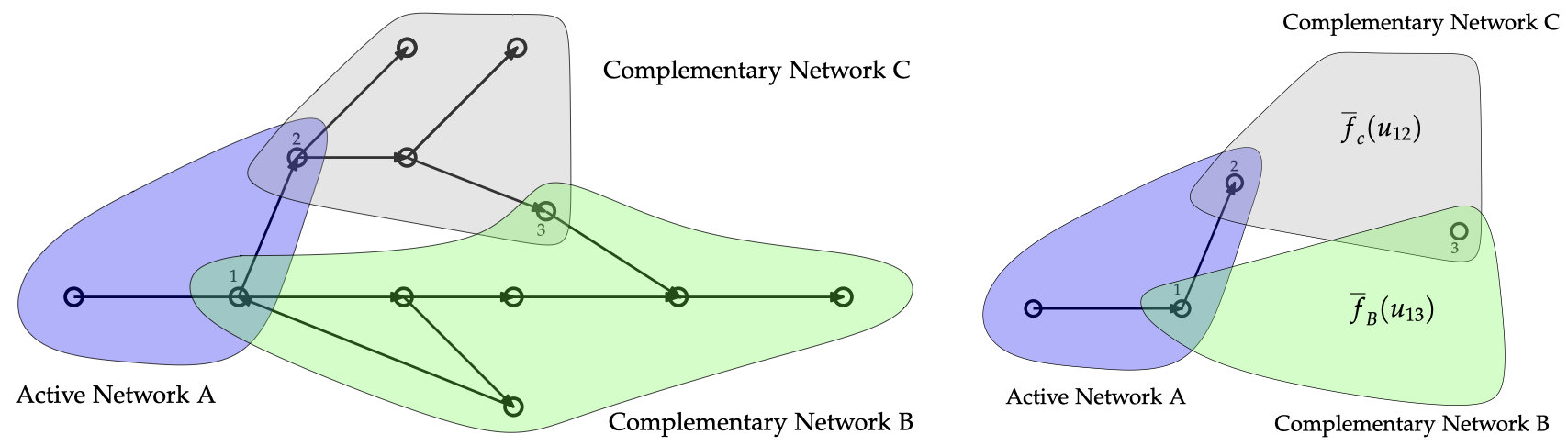Gas Network Image For the development of surrogates, we intend to use machine learning based models such as physics-informed neural networks (PINNs). These capture the gas flow dynamics while being much simpler to compute than standard techniques.

📝 Publications and preprints

  1. Mundinger, K., Zimmer, M., and Pokutta, S. (2024). Neural Parameter Regression for Explicit Representations of PDE Solution Operators. [arXiv]
    [BibTeX]
    @misc{NeuralRegressionPDE2024,
  archiveprefix = {arXiv},
  eprint = {2403.12764},
  primaryclass = {cs.LG},
  year = {2024},
  author = {Mundinger, Konrad and Zimmer, Max and Pokutta, Sebastian},
  title = {Neural Parameter Regression for Explicit Representations of PDE Solution Operators}
}
  2. Göß, A., Martin, A., Pokutta, S., and Sharma, K. (2024). Norm-induced Cuts: Optimization with Lipschitzian Black-box Functions. [URL] [arXiv]
    [BibTeX]
    @misc{gmps_nic_23,
  url = {https://opus4.kobv.de/opus4-trr154/files/518/nic_preprint.pdf},
  archiveprefix = {arXiv},
  eprint = {2403.11546},
  primaryclass = {math.OC},
  year = {2024},
  author = {Göß, Adrian and Martin, Alexander and Pokutta, Sebastian and Sharma, Kartikey},
  title = {Norm-induced Cuts: Optimization with Lipschitzian Black-box Functions}
}